Lapszámok

2011 9. szám
- Dr. Csoknyai Tamás PhD:
Épületgépészeti és épületenergetikai szakirányok a Létesítménymérnök mesterszakon, a Debreceni Egyetemen - Dr. Zöld András:
„Városenergetikus” szakmérnök képzés – miért, miről? - Szabó Gábor:
Geotermális energiával működtetett abszorpciós hűtőgép és hőellátó vezetékének energetikai elemzése a hőforrás hőmérsékletének szempontjából - Dr. Garbai László - Dr. Jasper Andor PhD:
A matematikai rendszerelmélet feldolgozása és alkalmazása épületgépészeti optimalizációs feladatok megoldására 2. rész - Schlüter-Systems KG magyarországi képviselet:
Az energiahatékony fűtési rendszerek fűtőfelülete a Schlüter® - BEKOTEC - Gróman Attila:
Vákuumcsöves napkollektorok a Bosch-tól - Kovács Attila:
Fűtési rétegtároló = OSKAR - Fördős Norbert:
Vaillant termékújdonságok 2011-ben - Révai Mária:
Hangcsillapított szennyvízelvezető rendszerek - Koczka Péter:
Új generációs hőkamera - Kovács István:
Légtechnikai csövek – az új generáció - Szalay Zoltán:
HALTON újdonságok a klímagerendás légkondicionálásban
Hozzászólások
A matematikai rendszerelmélet feldolgozása és alkalmazása épületgépészeti optimalizációs feladatok megoldására 2. rész
Még nem érkezett hozzászólás!
Dr. Garbai László - Dr. Jasper Andor PhD
A matematikai rendszerelmélet feldolgozása és alkalmazása épületgépészeti optimalizációs feladatok megoldására 2. rész
A cikk első részében, amely a Magyar Épületgépészet 2011/3. számában jelent meg [7], megállapítottuk, hogy a sugaras távfűtő rendszerek tervezése rendszertani szempontból, illetve a matematikai rendszerelmélet formalizmusa szerint egy soros, szétágazó döntési rendszerrel modellezhető. Ezt a modellezést el is végeztük. Asoros és nemsoros, azon belül a szétágazó és az összeágazó rendszer döntési modelljét szemléltettük, és meghatároztuk a hozzájuk tartozó célfüggvényeket. Bemutattuk a soros rendszer optimalizációját előre- és visszafelé haladó rekurzióval.Amodellben ismertek a nyomvonal hoszszúságok és a térfogatáram-igények. Ezek függvényében keressük azokat a csőátmérőket, amelyekkel a beruházási költség éves leírása és az üzemeltetési költség minimális. Jelen cikkünkben bemutatjuk a modell konkrét alkalmazását és az optimalizáció végrehajtását a diszkrét, dinamikus programozás felhasználásával.
Hazánkban a távfűtő rendszerek sugaras vagy hurkolt felépítésűek. Az esetek nagyobb többségében sugaras, szétágazó rendszert építenek, mivel ezek hidraulikai méretezése könnyebb, bár a hurkolt rendszernél az ellátás biztonsága nagyobb.
Ahogy említettük, bemutatjuk egy soros, szétágazó távfűtő hálózat (2.1. ábra) optimalizációját. Ismertek a nyomvonal hosszúságok és a térfogatáram-igények. Ezek függvényében keressük azokat a csőátmérőket, amelyekkel a beruházási költség éves leírása és az üzemeltetési költség minimális.
2.1. ábra. Soros, szétágazó távfűtő hálózat modellje
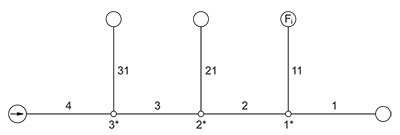
Az optimalizációt két lépcsőben végezzük el. Először végrehajtjuk az úgynevezett rendszerfüggetlen, szakaszonkénti optimalizációt. Ez a bázisát képezi a második lépcsőben a dinamikus programozással végrehajtandó optimalizációnak. A rendszerfüggetlen optimalizációval nyert eredmények a valóságos optimum alsó korlátját képezik, és ezáltal információval szolgálnak a dinamikus programozás állapotváltozói értéktartományának.










